Projects
Contents
- Sampling-based Algorithm for Optimal Motion Planning with Temporal Logic Specifications
- Motion-Planning in Dynamic Environment
- Trajectory Generation for Nonholonomic Vehicles
- Multiple Vehicles Task-Planning
- Motion-Planning with Temporal Logic Specifications for Nonholonomic Vehicles
- Incremental Path Repair Algorithm
- Object Recognition
- Game Hex AI
Sampling-based Algorithm for Optimal Motion Planning with Temporal Logic Specifications
Path planning algorithms with temporal logic specifications is known to be very hard from the computational point of view especially considering kinematic/dynamic constranits. Inspired from RRT*, I developed a “multiple layers sampling tree” method for such planning problem. The algorithm is probabilistic complete and monotonically converge to optimal.
In the example video, the task is to visit all three orange regions in the 100*100 map, use dubins’ car as vehicle model with a minimum turning radius=15. As the sampling tree grows, initial feasible path marked as red path, and update the solution when better path (black path) is found.
Motion-Planning in Dynamic Environment
In this topic we try to solve a motion planning problem that for a vehicle to achieve complex tasks but assume the environment is changing during the time such as some moving targets and moving obstacles.
Like the example video below, the task for the vehicle(red) is to reach some moving targets(yellow) in a certain order, and avoid moving obstacles(brown), also there are some doors in the environment open and close in some time.
The basic idea is from previous projects but add another time dimension in the search space, and build a switch policy that switch searching between dynamic space and static space to save computation time.
Trajectory Generation for Nonholonomic Vehicles
Cell decomposition-based path planning gives a sequence of cells but not actual trajectory, so I developed a sampling based algorithm to converge a optimal trajectory in the sequence of cells with kinematic constraint(in the example below, the vehicle has a minimum turning radius). Based on the Curvature-Bounded Traversability Analysis(CBTA) technic, the sampling space only on the edge of cells, this way the computation reduced dramatically.
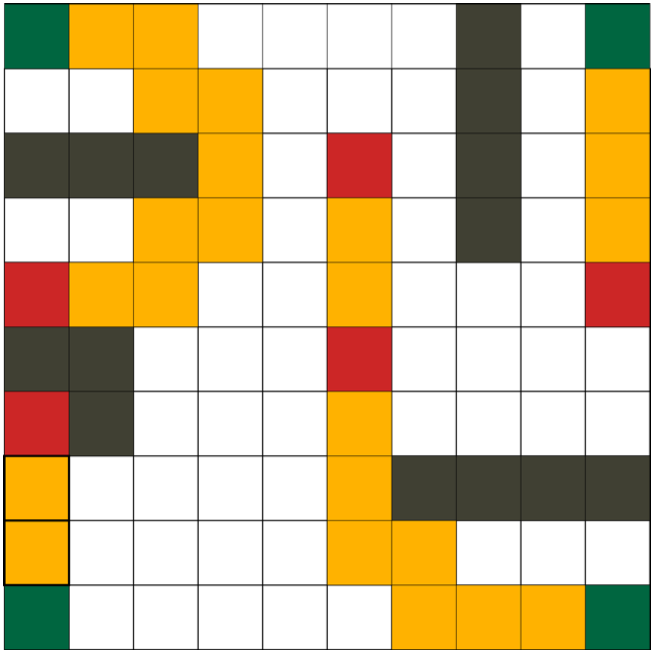
Multiple Vehicles Task-Planning
The challenge to extend single vehicle motion planning to multiple vehicles case is to handle the computation, especially with kinematic constraint. An incremental motion planning algorithm was developed for a group of vehicles could accomplished a global task.
In the example below, the task for the four vehicles(green) is to visit all the target regions(red) in the environment, and optimal paths(orange) are found.
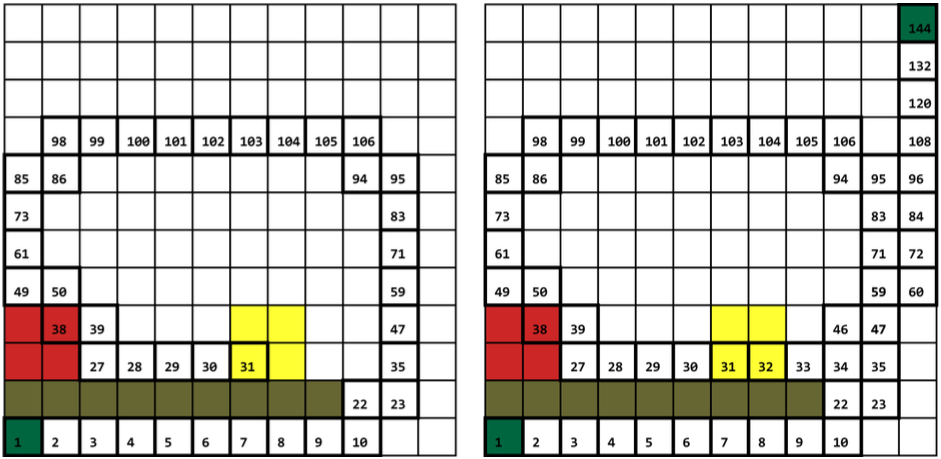
Motion-Planning with Temporal Logic Specifications for Nonholonomic Vehicles
Major part of my PhD research. Firstly, we are interested in the optimal motion planning and control problem, which involves finding control inputs (e.g. steering, throttle) that enable the vehicle’s desired motion. Optimal control theory has been studied for over three hundred years, but new computational strategies are required to develop real-time algorithms.
Secondly, we are interested in the intelligent control problem, which involves developing and integrating artificial intelligence (AI) algorithms with control algorithms to enable the vehicle to achieve complex tasks specified in human-like language (e.g. get me to my workplace ASAP, drop my friend close to his workplace, find a cheap parking spot and wait until I need you again; also save gasoline as much as possible). AI and automatic control have been traditionally disparate academic disciplines; furthermore, AI and control problems are formulated using fundamentally different mathematical tools, which makes their integration challenging.
Instead of point to point path search, the examples below show how a vehicle with a minimum turning radius accomplish a task. The first task requires the vehicle not only that the regions red and yellow be both visited, but also that the region red be visited first. The second task requires the vehicle returns to either one of the green regions after visiting red and yellow.
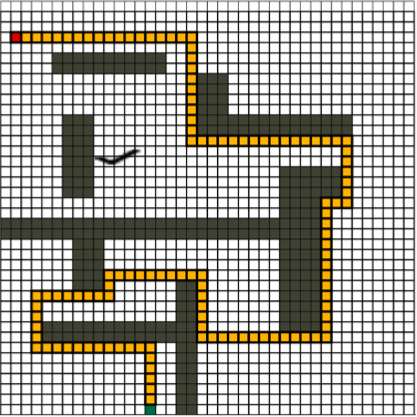
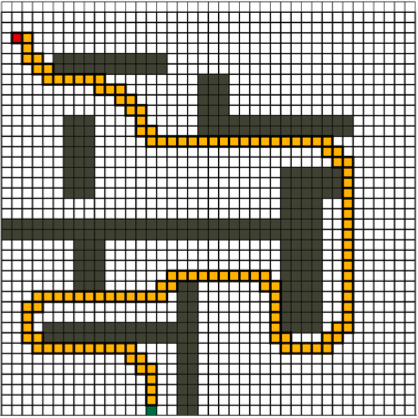
Incremental Path Repair Algorithm
Path planning with dyanmic or kinematic constraints. An incremental algorithm has been developed to find a point to point optimal path with dyanmic or kinematic constraints of the vehicle.
In the example below, we need to find a path from green point to red point for a vehicle which has a minimum turning radius. The left is the A* algorithm solution, and it’s not feasible for our vehicle model, we “repair” such path into the right one. The solution converge to optimal given enough computation time.
Object Recognition
Course project, aim to develop a method to recognize a certain object. A frisbee as testing object, first we narrow down the domain using color filter and contour detection.

Then apply Speeded Up Robust Features(SURF) algorithm for feature detection.

